I am having some doubts as to whether -fft is producing the correct phase data. (Or perhaps documentation is incomplete as to what it is _supposed_ to produce).
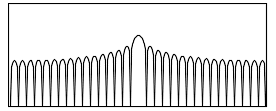
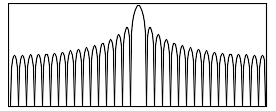
I'm looking at the DFT of simple straight line segment that can be used to simulate a motion blur:

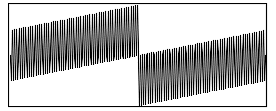
I reproduce the above image using IM then do the DFT in phase/magnitude and get the two layers as png files.
Code: Select all
length=15;
name=motion$length;
convert -size ${ww}x${ww} xc:black -fill white \
-draw "line $(($half-$length/2)),$half $(($half+$length/2)),$half" -alpha off \
${name}.png
mean=`convert ${name}.png -format "%[mean]" info:`
mask=$name.png
ww=`identify -format "%w" $mask`
half=$(($ww/2))
# same as above to get four images Real,Imaginary
convert \( $mask -roll -${half}-${half} -fft -level 0x$mean \) \
\( cameraman.png -fft \) \
cameraman_${name}-fftMP.png
convert \( $mask -roll -${half}-${half} -fft \) \
${name}-fftMP.png

Latest on-line doc tells me the following:
I'm using a HDRI build , so this statement (or it's implied inverse) is not true. The above plot is not in the range 0-2*pi !http://www.imagemagick.org/script/comma ... 0na4pidop4
Phase values nominally range from 0 to 2*π, but for non-HDRI compilations of ImageMagick, the phase image is scaled to span the full dynamic range.
Code: Select all
convert -version
Version: ImageMagick 6.7.4-0 2012-01-03 Q16 http://www.imagemagick.org
Copyright: Copyright (C) 1999-2011 ImageMagick Studio LLC
Features: HDRI
Second , this image has only three values: black and white and 50%grey. This would seem an improbably result unless this is just near zero noise being scaled up , even then it's dubious.
Finally , unless I am confusing thing I have other sources that indicate the imaginary part is a cosine and that makes the phase a smoothly rotating angle not this staccato all or nothing.
http://mathworld.wolfram.com/SincFunction.html says : {sinc(x),cos(x)}
also I have a locally built DFT routine released by arachnoid, that work very well on 1-D (audio) signals.
http://www.arachnoid.com/signal_processing/fft.html
Using the latter to transform a rectangular step I get pure cosine in the imaginary.
Using IM , I get a black square.
Code: Select all
convert \( $mask -roll -${half}-${half} +fft \) ${name}+fft.pngThis may be "small but acceptable" errors and maybe not . When chasing out ringing in FFT processes you need to be nit-pickingly precise. Undocumented features (if that is the case) and incorrect statements in the doc do not help help diagnose problems.
Any clarifications as to what extent all this is a bug or a feature would be helpful.
regards.