Legacy ImageMagick Discussions Archive

anthony wrote:...
As for 2 lobe support. Really if you are going to use 2 lobe, my thinking is why use A Windowed sinc at all, you may as well use a cubic filter

There is some weak evidence that if you are downsampling, a well-chosen 2-lobe windowed Sinc is better than any BC-cubic.
When I remember where I got this from, I'll post again.
P.S. Maybe it was for EWA?

anthony wrote:... all the other filters remain 4 lobed by default. That includes Raw Sinc or Fast Sinc as 4 lobes by default though they probably should also should be 3 lobe...

IMHO, Raw Sinc/Fast Sinc should be at least 4 lobes. Reason: Having a window function that does not vanish at the end of its extent (like Box=none) leaves visible artifacts. Such artifacts are decreased by using more lobes, since the filter is already small near the end of its extent, and consequently it's less important to window it to start with.
This is why Hamming and raw Sinc/SincFast should be 4 lobes at least, as well as Bartlett, because of the slope discontinuity it introduces at the center instead of at the window boundary.
There are two factors at play here:

If the window is sufficiently smooth so as not to introduce gradient discontinuities (this means that it vanishes at the end of the window, and it has a vanishing slope at the center), use more lobes if it "tapers" a lot, less otherwise.
Otherwise (if the window introduces gradient discontinuities) use more lobes.

If one only uses 3 or 4 lobes as defaults, this means that only Lanczos, Cosine and Welch are 3-lobe (if the cut-off for 3-lobe is Lanczos), and all the others should have 4 lobes.
Kaiser, depending on the parameter, either has a jump at the window edge, or it's tapered, so it should be 4-lobe either way.
Of course, the above are rules of thumb. Mix and match of lobes and windowing functions gives filters with slightly different properties. (As mentioned, Hann 2 works well when enlarging images that are "sharp".)

I left both Hann and Hamming as 4 lobe as that is what they were in "zoom", and as they are tapered (though one with a non-zero offset) I don't see the need to change it.

And only Lanczos, Welch, and Cosine have been given a 3 lobe support by default.

I have added a link to this topic in the appropriate section of IM Examples.
The Various Windowing Filters
http://www.imagemagick.org/Usage/resize ... _windowing

As an addendum to the window filters guide in IM Examples. I now not only graph the windowing filter over a normalized windowing range...


But I now also show a graph of the windowing function scaled over the default support range for that filter (according to the tapered/untappered classification)...
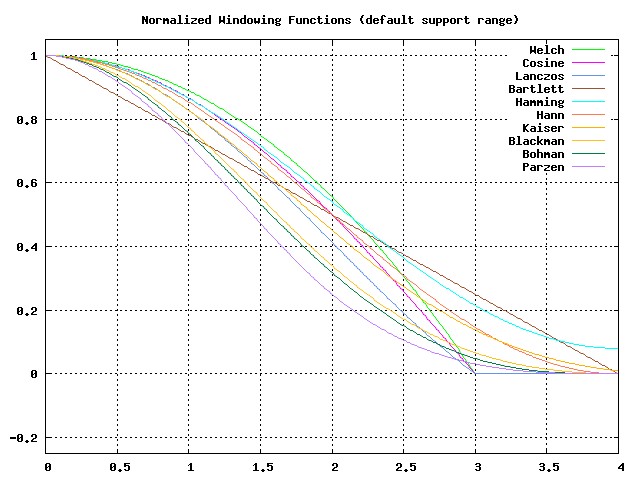
(may take an hour or so to appear)

This graph clearly shows how the adjustment causes the untapered the windowing filters to have a very similar rolloff, though amazingly the ordering of the filters has not changed much. Parzen still has the highest roll off, Welch the slowest, and Lanczos is still (or more so) in the very middle of the pack, (and has a smaller support for faster processing).

The biggest difference is that Hamming now has the second least amount of roll off, and it's non-zero taper is much more prominent.

The graphs and restructure of the IM Examples section is in
IM Examples, Resampling Filters, The Various Windowing Filters
http://www.imagemagick.org/Usage/filter/#windowing

Here is a funny coincidence:
The very first ranking shown in the Masters thesis of my student Adam Turcotte (he's polishing the final release)---and, here, you need to realize that such rankings are highly sensitive to "experimental conditions" and so should be taken with a large grain of salt---ranks all the 4-lobe versions of the various windowed-Sincs you show in your graph above the 3-lobe versions (and 2-lobe versions) EXCEPT for Cosine, Lanczos and Welch. This very first ranking could be argued to be the most "reliable" or "all encompassing".
I'll make sure to link the thesis when it's finally published.
(The three tested Kaiser windows are different from the built-in ones, I think.)

Anthony:
These are informative graphs, and I'm glad for the addition.
Why I also would like to see is a plot of the results at the "default" scaling, like in the second plot, of multiplying by the truncated Sinc with the default number of lobes. That is, the "overall kernel".
And then, a plot (of a slice of) the impulse response, at the same scale. Because, really, it's the impulse response that matters. The windowed-Sincs and Jincs are just a way to get a particular impulse response. (Well, also frequency response. And of course we're ignoring 2D effect.)

anthony wrote:...
The biggest difference is that Hamming now has the second least amount of roll off, and it's non-zero taper is much more prominent.
...

which is why I don't ever use or recommend Hamming. You can actually see the "break" in image resizing results.
I actually never use a window function that does not ensure that the final windowed-Sinc (or Jinc) is not C^1 (continuously differentiable, that is, with a continuous "slope" in all directions, at every point). So, Hamming and Bartlett are disqualitifed from the get go. With some choices of the key parameter (alpha, or beta), Kaiser "almost" gives a C^1 final result. But I disqualify it anyway just to be safe (and I'm always tempted to undo this technical disqualification). You can see the tiny "jump" at the end of the window in the second plot, quite clearly.

NicolasRobidoux wrote:Anthony:
These are informative graphs, and I'm glad for the addition.
Why I also would like to see is a plot of the results at the "default" scaling, like in the second plot, of multiplying by the truncated Sinc with the default number of lobes. That is, the "overall kernel".

The final produce has always been present using default support/lobes setting. But windowed sincs are all so on top of each other that it is very hard to see how they differ, even in the larger view. I have been thinking of a 'magnification' view of the first two lobes
just so that the differences can be seen more clearly.

And then, a plot (of a slice of) the impulse response, at the same scale. Because, really, it's the impulse response that matters. The windowed-Sincs and Jincs are just a way to get a particular impulse response. (Well, also frequency response. And of course we're ignoring 2D effect.)

I am not certain what you mean by this request. The profile graph of a single pixel impulse image?

anthony wrote: I am not certain what you mean by this request. The profile graph of a single pixel impulse image?

Exactly, so that we see the effect of "normalizing by the sum of the weights at every location". With no clipping (in "HDRI").
This is a curve.
Note: When the kernel defines a partition of unity, there is no difference with the kernel. (For example, with Triangle, the Keys Cubics, Quadratic B-spline.)
With the windowed Sincs (and Jincs), there is a difference, which I guess can be considerable (?).
Of course, it should be shown as a surface in 2D, but it's easier to grasp minor differences in a "slice".

Nicolas wrote:Of course, it should be shown as a surface in 2D, but it's easier to grasp minor differences in a "slice".

There is a nice 2D image to 3D surface graph function in ImageJ that I used for some of my FFT images. See http://www.fmwconcepts.com/imagemagick/ ... properties

Don't know if that would be helpful or not?

NicolasRobidoux wrote: I actually never use a window function that does not ensure that the final windowed-Sinc (or Jinc) is not C^1 (continuously differentiable, that is, with a continuous "slope" in all directions, at every point).

Let me modulate this binary statement:
When enlarging decent quality natural images a lot, I never use, and do not recommend, methods that are not C^1 (unless, possibly, they are "almost C^1", like madVR's Jinc3 and Jinc3 AR).
In other words, there may be exceptions to "never". But this is nonetheless a rule of thumb I need to have a good reason to deviate from.

You mean a profile, something like I did with a gaussian that was clipped by too small a support (as it was in earlier versions of IMv6)
http://www.imagemagick.org/Usage/filter/#support

Done as a demonstration of the direct aliasing that results from a off clipping of the support.

What I mean is that, when enlarging a lot, I don't recommend filters that have a significant "jump" (which indeed happens if you clip the support of the Gaussian too soon, a good example indeed being http://www.imagemagick.org/Usage/filter/#support) or a significant jump in slope (a "corner"), like bilinear or Kaiser with some of the choices of parameter.
When resizing just a little, such things don't matter much. Nearest neighbour, when resizing just a little, is actually a good choice if you want sharpness.